Core Math Worksheets
Fraction Worksheets
Algebra
Other Worksheets
Place Value
Percentages
Rounding Numbers
Ordering Numbers
Standard, Expanded, Word Form
Mean Median Mode Range
Ratio Worksheets
Probability Worksheets
Roman Numerals
Factorization, GCD, LCM
Prime and Composite Numbers
Pre-Algebra
Geometry Worksheets
Blank Clocks
Telling Analog Time
Analog Elapsed Time
Greater Than and Less Than
Money
Arithmetic Sequences
Geometric Sequences
Venn Diagram
Graph Worksheets
Measurement & Conversions
Patterns and Puzzles
Color by Number
Holiday & Seasonal
Early Learning
Printables
Calculators
Math Worksheets by Grade
Worksheet News
Two Step Equations
The two step equations worksheets on this page include problems with integers, decimals and fractions for a variety of math operations. These beginning algebra worksheets are appropriate practice for 6th grade, 7th grade and 8th grade students. Full answer keys are included on the second page of each PDF file.
Two Step Equations with Decimals
Two Step Equations with Fractions
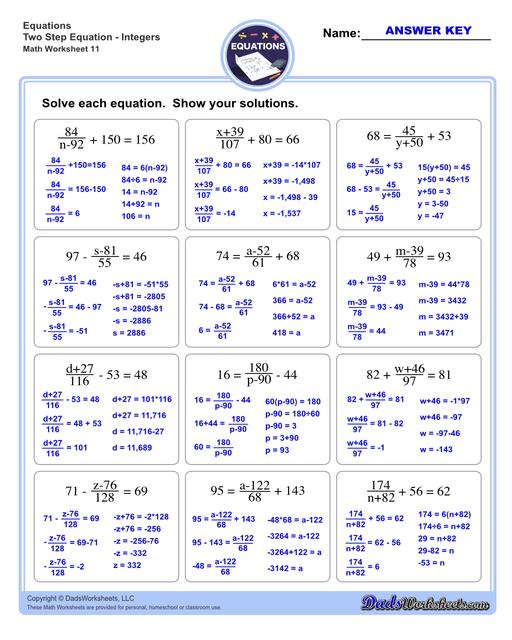
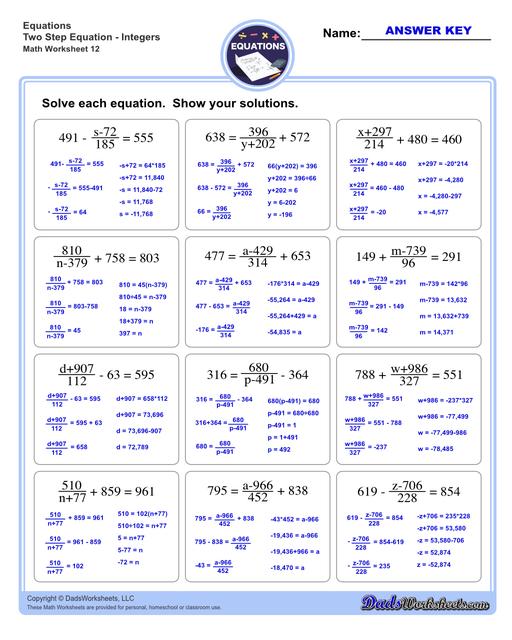
Two Step Equations with Integers
Two Step Equations
These worksheets will help students practice their algebraic skills in solving two step equations including integers, fractions, and decimals. The first set of worksheets start with solving basic algebraic equations involving integers - all operations included from addition, subtraction, multiplication and division.The second set involves fraction problems and finally the last set will let you solve decimal problems from small numbers to bigger ones.All of these worksheets include answer keys with solutions! Go ahead and check out these worksheets or continue reading below to discover tips and more facts about 2 step equations.
What Are Two Step Equations?
With the meaning in its name – a two step equation is an algebraic equation that will take you two steps to solve for the unknown variable. You've solved the equation when you get the variable by itself, with no numbers in front of it, on one side of the equal sign.Once you've solved it, you can the check the equation by substituting your final answer to the variable and if both sides are equal then you've found the value of the variable that makes the equation true.Let us check how…
Example:
3x + 1 = 10
3x = 10 - 1
3x = 9
x = 9/3
x = 3
To check if the equation is true, substitute “x” with “3”.
3x + 1 = 10
3(3) + 1 = 10
9 + 1 = 10
10 = 10
Both sides are equal, making the equation “3x + 1 = 10” true.
Solving Two Step Equations
Positive and Negative Integers Equations
I’ve discussed about positive and negative integers in my post about one step equation, but let me refresh you again.When we hear integers, some of us will say “these are whole numbers.”but what exactly are integers and what includes whole numbers?Integers are whole numbers, but they also include negative numbers, including 0.It is a number with no decimal or fractional part.These are all of the whole numbers ( 2, 4, 5, 7…) and their opposites (-2, -4, -5, -7…) and don’t forget, 0 is also an integer.0 is neither a positive nor a negative integer. Anything above 0 is a positive integer, and anything below it is a negative integer.There you have it!Now that we already know about what exactly integers are, let us do some examples and know the step by step procedure to solve different kinds of two step equation problems.After we’re done with all these examples, solving two step equations will be a piece of cake for you!
Steps to Solving an Equation
Example 1:Integers
4 + 2x = 8
Step 1:Isolate “x” by subtracting “4” from both sides of the mathematical sentence and this will cancel out the 4 on the left side part of the equation. Remember this:When moving a positive number to the opposite part of the equation, positive should turn into negative; “4” becomes “-4”. This will make the equation as shown below.
4 + 2x - 4 = 8 - 4
2x = 4
Step 2:Divide both sides by 2 to cancel out “2” in “2x”
2x/2 = 4/2
x = 4/2
Step 3:Solve for the division question “4/2”
x = 2
To check your answer, substitute the variable “x” with “2”
4 + 2x = 8
4 + 2(2) = 8
4 + 4 = 8
8 = 8
Our answer “x = 2” is correct because both sides of the equation are equal.
Example 2: Integers
4 - 2x = 8
Step 1:Subtract “4” on both sides.
4 - 2x - 4 = 8 - 4
-2x = 4
Step 2: Divide both sides by “-2”
-2x/2 = 4/2
-x = 2
Step 3:Again, let me remind you about the rule that the “x” should never be negative. In the example given above, “x” is negative.To change this, put the “-” sign onto the other side, to the “2”. To conclude, the answer is “-2”.
x = -2
Let us check if our answer will make the equation true.Substitute the variable “x” with “-2”.
4 - 2x = 8
4 - 2(-2) = 8
4 + 4 = 8
8 = 8
Our answer “x = -2” is correct because both sides of the equation are equal.
Example 3:Integers
x/2 + 4 = 9
Step 1:Start by simplifying the equation by subtracting “4” on both sides.
x/2 + 4 -4 = 9 - 4
x/2 = 5
Step 2:Multiply both sides by “2”.This will cancel out “2” on the left side of the equation.
x/2 * 2 = 5 * 2
x = 5 * 2
Step 2:Solve for “5 * 2”
x = 10
To check, substitute “x” with our final answer “10”
x/2 + 4 = 9
10/2 + 4 = 9
5 + 4 = 9
9 = 9
Our answer “x = 10” is correct because both sides of the equation are equal.
Example 4:Integers
x + 3 - 2 = 10
4
Step 1: Add “2” on both sides to simplify the equation.
x + 3- 2 + 2 = 10 + 2
4
x + 3= 12
4
Step 2: Mutliply both sides by “4” to cancel out “4” on the left side of the equation.
x + 3 * 4 = 12 * 4
4
x + 3 = 48
Step 3:Subtract “3” from both sides.This will leave you with the final answer that is “x = 45”.
x + 3 - 3 = 48 - 3
x = 45
Let’s now check our final answer by substituting “x” with “45”
x + 3- 2 = 10
4
45 + 3- 2 = 10
4
48- 2 = 10
4
48= 10 + 2
4
12 = 12
We got it right again!Both sides of the equation are equal.
Two Step Equations With Decimals
Now that we have practiced solving problems on positive and negative integers, solving for decimal problems will be easier.Same rules apply and just solve the problem as you would solve any two step equation.
Let’s go try some examples at solving two step equations involving decimals this time.
Example 1:Decimals
3.1x + 2 = 5.5
Step 1:Subtract “2” from both sides of the equation.
3.1x + 2 - 2 = 5.5 - 2
3.1x = 3.5
Step 2:Divide both sides by “3.1”.
3.1x ÷ 3.1 = 3.5 ÷ 3.1
x = 3.5 ÷ 3.1
Step 3:Do the calculations to solve for x.
x = 1.13
Go ahead and substitute “x” with “1.13” to check our answer.
3.1x + 2 = 5.5
3.1(1.13) + 2 = 5.5
3.1(1.13) + 2 - 2 = 5.5 - 2
3.1(1.13) = 3.5
3.5 = 3.5
Yes, our answer is correct because both sides of the equation are equal.
Example 2: Decimals
12.1x = x - 9.3
Step 1:Combine like terms.Move “x” to the left hand side of the equation.
12.1x - x = -9.3
11.1x = -9.3
Step 2:Divide both sides by “11.1” to isolate “x”.
11.1x ÷ 11.1 = -9.3 ÷ 11.1
x = -9.3 ÷ 11.1
Step 3:Solve for x.
x = -0.8378
Let’s check our answer.Substitute “x” with “-0.8378”
12.1x = x - 9.3
12.1 (-0.8378) = -0.8378 - 9.3
-10.1378 = -10.1378
Our answer “x = -0.8378” is correct because both sides of the equation are equal.
Two Step Equations With Fractions
The procedure for solving 2 step equations involving fractions is the same as integers and decimals.If you have mastered solving 2 step equations for integers and decimals, then solving for fractions will be easy too.The first goal is still the same: to isolate the variable on one side. Let me walk you through the steps by solving these example problems below…
Example 1: Fraction
x + 1/2 = 3/4
Step 1:Isolate “x” by subtracting “1/2” from both sides of the equation.This will cancel out 1/2 on the left-hand side of the equation and will leave “x” alone.
x + 1/2 - 1/2 = 3/4 - 1/2
x = 3/4 - 1/2
Step 2:Find the LCM (least common multiple) of the denominators “4” and “2”.In this case, the LCM is “4”.The smallest positive number that is both divisible by “4” and “2”.Adjust the fractions based on LCM.
x = 3/4 - 2/4
Step 3:Now that the denominators are the same, combine the fractions “3/4” and “2/4”.
The numerators “3” and “-2” will become “1” since “3 - 2” is “1”.
x = 1/4
Let’s now check our final answer by substituting “x” with “1/4”.
x + 1/2 = 3/4
1/4 + 1/2 = 3/4
1/4 + 2/4 = 3/4
3/4 = 3/4
Our answer “x = 1/4” is correct because both sides of the equation are equal.
Example 2:Fraction
2/3 x + 1/2 = 1/3
2/3 x + 1/2 - 1/2 = 1/3 - 1/2
2/3 x = 1/3 - 1/2
2/3 x = 2/6- 3/6
2/3 x = -1/6
36
2/3 x (3) = -1/6 (3)
2x = -3/6
x = -3/6 ÷ 2
x = -3/12
x = -1/4
Time to check if we got the answer right… Substitute with “-1/4” for “x”.
2/3 x + 1/2 = 1/3
2/3* -1/4 + 1/2 = 1/3
2/3* -1/4 + 1/2 - 1/2 = 1/3 - 1/2
2/3 * -1/4 = 2/6 - 3/6
2/3 * -1/4 = -1/6
1/3 * -1/2 = -1/6
-1/6 = -1/6
Yes, both sides are equal so our answer “-1/4” is correct.
Solving 2 step equations is extremely easy right? The key is practice! practice! practice!Just remember the steps and don’t forget about changing the signs when you move the numbers.If you are still feeling a little lost, that’s okay.You can go over our 2 step equations examples again above or check our pdf worksheets whenever you’re ready. All of our worksheets have answer keys and solutions so you can always validate your answers. Good luck!