Core Math Worksheets
Fraction Worksheets
Algebra
Other Worksheets
Place Value
Percentages
Rounding Numbers
Ordering Numbers
Standard, Expanded, Word Form
Mean Median Mode Range
Ratio Worksheets
Probability Worksheets
Roman Numerals
Factorization, GCD, LCM
Prime and Composite Numbers
Pre-Algebra
Geometry Worksheets
Blank Clocks
Telling Analog Time
Analog Elapsed Time
Greater Than and Less Than
Money
Arithmetic Sequences
Geometric Sequences
Venn Diagram
Graph Worksheets
Measurement & Conversions
Patterns and Puzzles
Color by Number
Holiday & Seasonal
Early Learning
Printables
Calculators
Math Worksheets by Grade
Worksheet News
Exponent Rules
Understanding rules for using exponents in algebraic equations is crucial for middle school age students. It forms the foundation for more complex mathematical concepts in higher grades such as logarithms or calculus. Mastery of exponents enhances problem-solving skills, critical thinking, and fosters a deeper understanding of mathematical relationships, aiding academic growth and future career opportunities, and the resources on this page are here help!
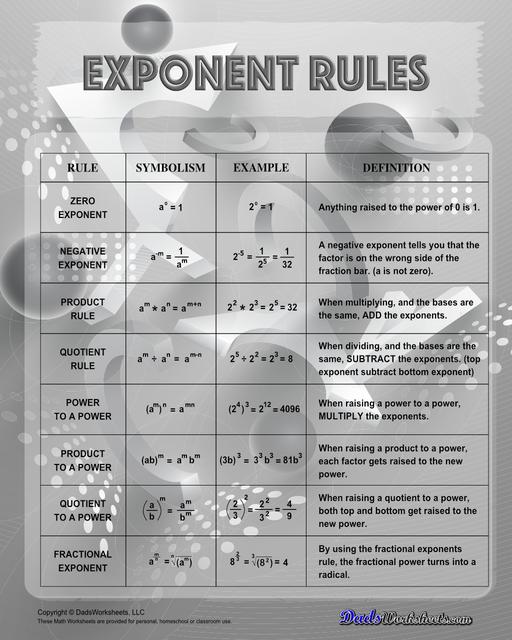
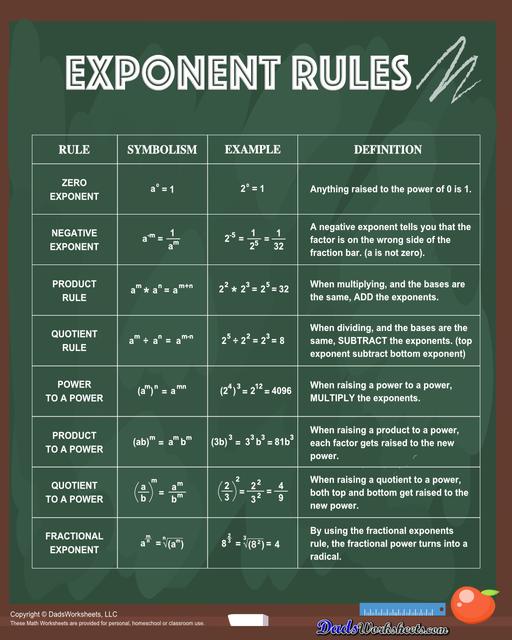
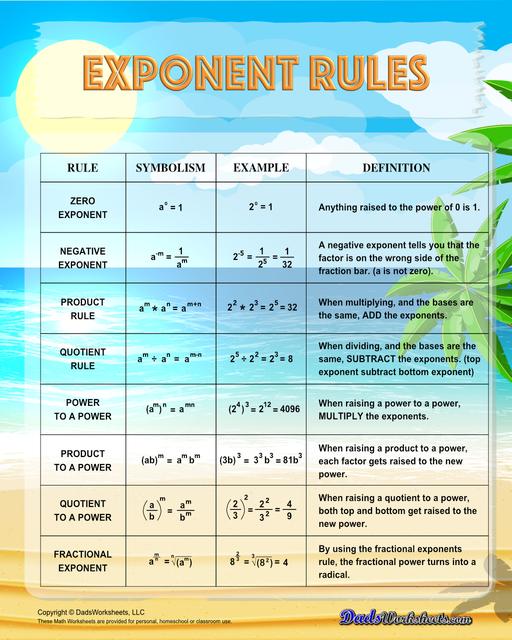
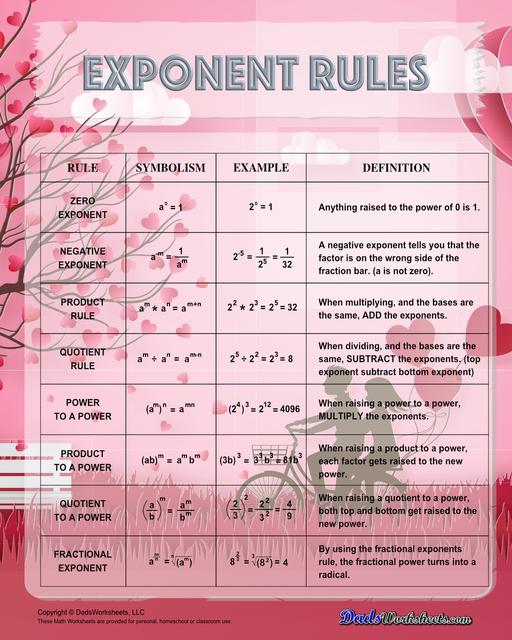
Exponent Rules Chart
Each exponent rules chart on this page summarizes how to use the power rule, fraction rule, product rule, the negative rule, log to exponents and more! The laws of exponents illustrate how to simplify numbers using the properties of exponents in multiplication and division terms. Having one of these anchor charts on hand is a great way to start memorizing these useful exponent facts!
Exponent Rules Chart
Exponent Rules Worksheets
These exponent rules worksheets provide practice using the power rule, fraction rule, product rule, the negative rule, log to exponents and more! Learn how to simplify numbers with exponents and see how they relate to fractions, decimals and roots using these PDF worksheets with answer keys.
Fractional Exponent Rule
Negative Exponent Rule
Power to a Power Exponent Rule
Product Exponent Rule
Product to a Power Exponent Rule
Quotient Exponent Rule
Quotient to a Power Exponent Rule
Exponent Rules
The worksheets on this page will let students simplify expressions and solve problems while using the laws of exponents or exponent rules. These worksheets are perfect for children in the 4th Grade, 5th Grade, 6th Grade, 7th Grade, and 8th Grade.
All of these worksheets include answer keys and solutions! Go ahead and check out these exponent rules worksheets or continue reading below. You may also print one of our high resolution Exponent Rules Charts. This is a perfect guide while you are still starting to learn about the eight laws of exponents.
What is an Exponent?
In the same way that the multiplication symbol denotes repeated addition, the exponent denotes repeated multiplication. Exponents provide a concise way to express repeated multiplication and simplify equations to make them easier to read.
Writing a number in exponential form refers to simplifying it to a base with a power. The number being raised by a power is known as the base, while the superscript number above it is the exponent. Exponents are values that show how many times we multiply a base number by itself, while power means raising a base by a power. For example, 2^3 is the power where 2 is the base and 3 is the exponent.
And as we delve into the world of exponentiation, understanding the rules governing these powerful mathematical entities becomes crucial for simplifying expressions and solving equations efficiently. Exponent rules also simplify calculating extremely large or extremely tiny quantities. There are eight laws of exponents and each rule shows how to solve different types of math equations and how to add, subtract, multiply and divide exponents. Let me walk you through these rules one by one…
Zero Exponent Rule
Anything raised to the power of 0 is 1. This rule can be justified by considering that any non-zero number multiplied by its reciprocal equals 1.

In our example above, 2 is the base and 0 is the exponent. 2 raised to the power of 0 is equal to 1. When we raise 2 to the power of 0, that means we are multiplying the number 2 by itself zero times, and that means we're not multiplying anything at all. So, the reason that any number to the zero power is one is because any number to the zero power is just the product of no numbers at all, which is the multiplicative identity, 1.
Negative Exponent Rule
A negative exponent tells you that the factor is on the wrong side of the fraction bar. So when an expression with a negative exponent is moved to the denominator (bottom), the exponent becomes positive. This rule facilitates expressing quantities with negative exponents in a more convenient form. In other words, the negative exponent rule tells us that a number with a negative exponent should be put to the denominator, and vice versa. This means that if the power is negative, it has to change its place from numerator to denominator or denominator to numerator.

Product Rule
One of the fundamental rules of exponents involves the multiplication of terms with the same base. The product rule states that when you multiply two expressions with the same base, you can combine the exponents by adding them. This rule underscores the concept that repeated multiplication can be condensed into a single exponentiated expression. To multiply two expressions with the same base, add the exponents while keeping the base the same. Note that bases must be the same to use the product rule. Refer to our example below…

To simplify the given example above, identify first the terms with common bases. In our example, the common base is 2. Next, identify the exponents of 2. In this case, the exponents are 2 and 3. Add the exponents 2 and 3. The simplified expression is 2 raised to the power of 5.
Quotient Rule
The quotient rule comes into play when we divide two expressions with the same bases. In this rule, the exponents are subtracted. Simply say, the quotient rule of exponents allows us to simplify an expression that divides two numbers with the same base but different exponents. This rule is also essential for simplifying fractions with exponential terms.

Look at our example above. Notice that the exponent of the quotient is the difference between the exponents of the divisor and dividend. 5 minus 2 is equal to 3.
Power To A Power Rule
The power to a power rule allows us to raise an exponentiated expression to another power by multiplying the exponents. This rule is particularly useful when dealing with nested exponents. The power to the power rule states that “If the base raised to a power is being raised to another power, then the two powers are multiplied and the base remains the same.” Let us use the example below to understand better:

In our given example above, 2 is the base while the exponents are 4 and 3. To simplify this, multiply the exponents 4 and 3. The answer is 12. Keep the same base, the result is 2 raised to the power of 12.
Product To A Power Rule
The Product to a Power rule is another way to simplify exponents. When raising a product to a power, each factor gets raised to the new power. In other terms, it is a multiplication expression raised, as a whole, to a power. Be sure to notice that this rule only works when the term inside the parenthesis is a single term (a product, without + or - signs separating them).

In our example above, there are two variables or constants that are being multiplied together, those are the 3 and b. The result of this multiplication problem must be raised to a power which in our given example is 3. Both 3 and b are raised to the power of 3, indicating that each element of the product is raised to the exponent outside the parenthesis. 3 raised to the power of 3 is 3x3x3 or 81. The answer is 81b^3.
Quotient To A Power Rule
When raising a quotient to a power, both top and bottom get raised to a new power. This means that the power of a quotient is equal to the power of each term in the numerator and denominator raised individually. The exponent outside of the parentheses is distributed to each term in the numerator and each term in the denominator. Here’s an example…

To simplify this expresion, the exponent 2 is distributed to both the numerator 2 and denominator 3. 2 raised to the power of 2 is 4, 3 raised to the power of 2 is 9. The simplified expression is 4/9.
Fractional Exponent Rule
If the exponent of a number is a fraction, it is called a fractional exponent. By using the fractional exponents rule, the fractional power turns into a radical. Refer to the example below.

When you have a fractional exponent, the numerator is the power and the denominator is the root. In the example given, 8 is the base and 2/3 is the exponent, where 2 is the numerator and 3 is the root. 8 raised to the power of 2 is 64, and the cube root of 64 is 4. Hence, the answer is 4.
By mastering these exponent rules, one gains a powerful toolkit for simplifying complex expressions and solving equations. These rules form the backbone of algebraic manipulation, enabling mathematicians and scientists to handle a wide range of problems with elegance and efficiency. As we navigate the realm of exponents, these rules become invaluable guides, unlocking the potential for concise and insightful mathematical expressions.
In summary, exponent rules are foundational principles in mathematics that offer a systematic and efficient way to handle expressions involving powers. Their significance extends across various disciplines, contributing to problem-solving, algebraic manipulation, and the development of mathematical models in both theoretical and applied contexts.
History of Exponent Rules
The history of exponent rules is intertwined with the development of mathematical notation and the evolution of algebra. Exponentiation as a mathematical concept has ancient roots, but the formalization of exponent rules occurred gradually over the centuries. Here's a brief overview:
The concept of repeated multiplication, which is the basis of exponentiation, can be traced back to ancient civilizations. Babylonian and Egyptian mathematicians used various methods for handling powers in practical applications, such as in geometry and measurement.
Ancient Greek mathematicians, including Euclid and Archimedes, made significant contributions to mathematical knowledge. While they did not use the modern notation for exponents, their work laid the groundwork for later developments in algebra.
During the Islamic Golden Age (8th to 14th centuries), scholars like Al-Khwarizmi and Omar Khayyam made substantial contributions to algebra. Al-Khwarizmi's "Al-Kitab al-Mukhtasar fi Hisab al-Jabr wal-Muqabala" (The Compendious Book on Calculation by Completion and Balancing) provided solutions to linear and quadratic equations, and it marked the beginning of systematic algebraic notation.
In the 16th century, the Renaissance saw the resurgence of interest in mathematical studies. Mathematicians like François Viète and John Wallis began using symbolic notations to represent mathematical operations. Viète, in particular, introduced letters to represent unknowns and constants.
The development of symbolic algebra continued, and mathematicians like René Descartes and Isaac Newton made significant contributions. Descartes introduced the modern notation for powers, using superscripts to denote exponents. Newton's work with calculus and binomial theorem further advanced the understanding of mathematical operations involving powers.
The concept of exponentiation and its rules became more formalized during the 18th and 19th centuries. Mathematicians like Leonhard Euler and Augustin-Louis Cauchy contributed to the understanding of exponent rules and their applications in calculus and number theory.
The 20th century witnessed the establishment of modern mathematical notation, including the familiar symbols used for exponentiation. Exponent rules, such as the product rule, quotient rule, and power rule, were systematically formalized and taught as part of standard mathematical education.
Throughout this historical progression, the understanding of exponent rules evolved alongside advancements in algebra, calculus, and mathematical notation. The development of these rules reflects the ongoing efforts of mathematicians to systematize and simplify mathematical operations, ultimately providing a powerful framework for handling expressions involving powers.