Core Math Worksheets
Fraction Worksheets
Algebra
Other Worksheets
Place Value
Percentages
Rounding Numbers
Ordering Numbers
Standard, Expanded, Word Form
Mean Median Mode Range
Ratio Worksheets
Probability Worksheets
Roman Numerals
Factorization, GCD, LCM
Prime and Composite Numbers
Pre-Algebra
Geometry Worksheets
Blank Clocks
Telling Analog Time
Analog Elapsed Time
Greater Than and Less Than
Money
Arithmetic Sequences
Geometric Sequences
Venn Diagram
Graph Worksheets
Measurement & Conversions
Patterns and Puzzles
Color by Number
Holiday & Seasonal
Early Learning
Printables
Calculators
Math Worksheets by Grade
Worksheet News
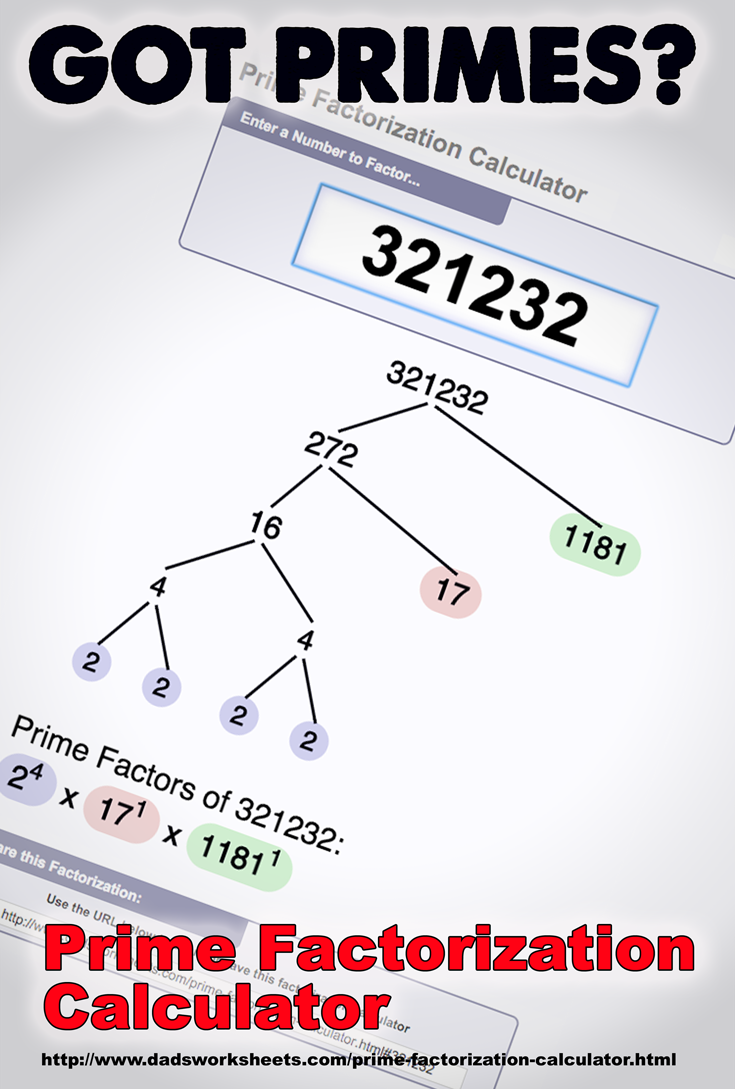
Prime Factorization Calculator
Using the Prime Factorization Calculator
This prime factorization calculator allows you to enter a composite number, and it produces a list of the prime numbers that, when multiplied, produce the original composite number. Use this factorization calculator to produce a factor tree, or just determine the list of primes that divide a given integer.
The factor tree produced by the site’s prime factorization calculator shows the prime values as highlighted nodes. Each prime factor is assigned a unique color, and the occurrences of the each prime factor correspond to the exponent on the same prime in the prime factorization in the canonical factorization shown below the factor tree.
There are many potential ways to produce a prime factorization, but some of them, especially those that start with small primes, produce very repetitive factor trees. The algorithm used by this prime factorization calculator starts it’s search for factors at the square root of the input and then checks for increasingly smaller factors. This will reuse a prime factorization of internal composite numbers more frequently and produces factor trees that are somewhat more compact (and elegant) than more naïve approaches.
Use the ‘Zoom’ button to highlight only the calculator on this page. That makes using this prime factorization calculator on smart boards or projectors in a classroom setting less distracting.
To understand what prime factorization is good for, it helps to start with the very nature of numbers and how their prime factors are used to create them.
What is a Prime Number?
A prime number is an integer that can be divided evenly only by the number 1 and itself. This is a fancy way of saying there isn't some other multiplication expression using only natural numbers that has as its product a prime number.
It's fairly easy to determine whether a small number is prime or not just by using the rules of divisibility and trial division or just plug the number into this prime factorization calculator!. However trying to determine whether a large number is prime or not is particularly hard. Factoring very large numbers that include very large primes is very difficult even with a computer and many years of time, and this is the basic reason why modern cryptography works.
What is a Composite Number?
Composite numbers are in some ways the opposite of prime numbers. While prime numbers cannot be divided by any other number besides one and themselves, a composite number MUST be divisible by at least one other number. Another way to say this is that a composite number is always the product of two (or more) prime numbers. Therefore, a composite number is composed of prime numbers.
This prime factorization calculator will take a composite integer and produce a prime factorization of that integer, listing the unique set of primes that compose a given product.
If the prime factorization contains only a single prime with an exponent of one, it is another way of saying that the integer is prime. This prime factorization calculator will identify such values immediately and tell you if they are prime.
Is 0 a Prime Number?
Zero is not a prime number, just plug it into the calculator and it'll tell you! Zero can be divided by any integer and give zero as a result, so it is not prime. It is also not composite because there are no two integers that can be multiplied together to get zero as their product.
It may surprise you, but some things like whether zero is prime or not can be occasionally controversial in mathematical circles. You can see some of the debate on the topic of where 0 is a prime number being debated here...
Is 0 a Prime Number?Is 1 a Prime Number?
One is not a prime number. One is also not a composite number. Because a prime must be divisible by exactly two factors, including one itself, the number one fails the test for primality because it has only a single factor. Because of this bit of complexity, the definition of prime number explicitly states that a prime must be larger than one, so one itself is by definition not prime, probably to prevent fourth grade math students' heads from spinning crazily in class.
One is also not a composite number. Remember a composite number must be the product of two primes. Since we know already one itself is not prime, and there isn't a even a pair of factors (much less a deeper prime factorization) for the number one.
What is Prime Factorization?
Any number can be uniquely represented as the list of prime numbers whose product is the value in question. This representation is called the prime factorization, or sometimes the canonical representation. A prime factorization is unique to the given value. There is exactly one prime factorization for any given positive integer, and that positive integer has only one prime factorization.
You can see some examples by entering values into the top box of this prime factorization calculator. The calculator will show one possible factor tree, plus the canonical form of the prime factorization as its output.
How to Find the Prime Factorization
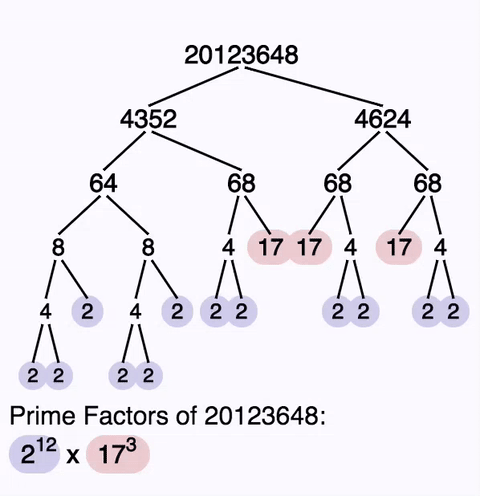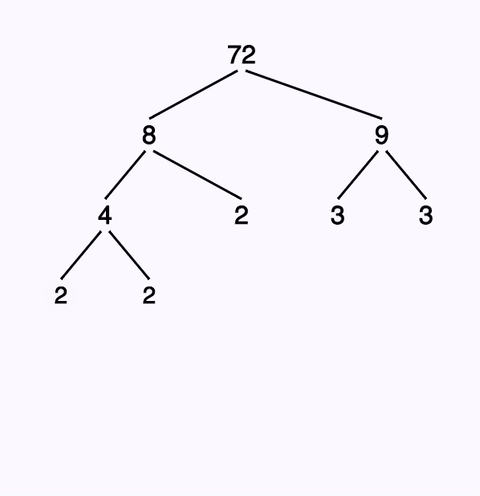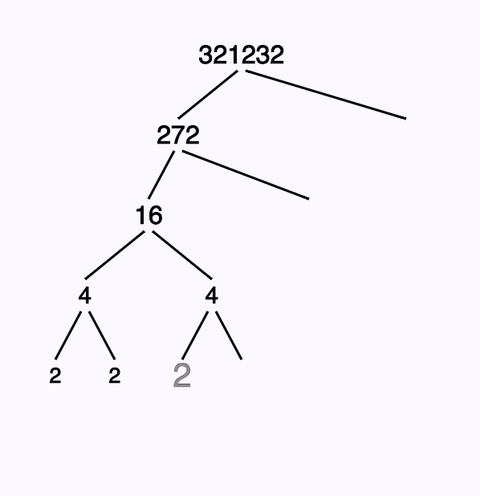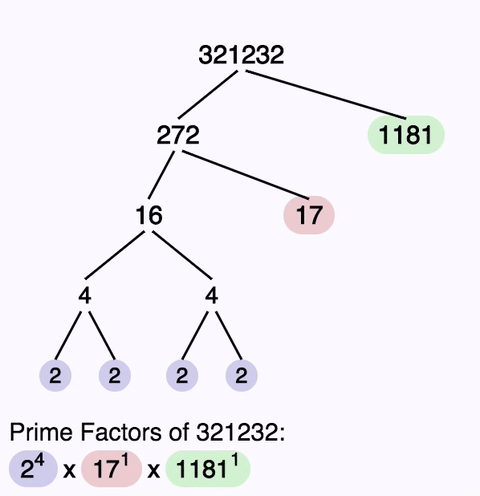
The easiest route to determining a prime factorization is start with a list of known primes and then divide them repeatedly into the quotients. For example, to find the prime factorization of 72, begin by dividing by the smallest prime 2…
72 ÷ 2 = 36
36 ÷ 2 = 18
18 ÷ 2 = 9
At this point, we’ve observed that 72 has three 2’s in it. So 2 is a prime in the factorization of 72, and it occurs three times. However, we can’t divide 9 by 2, so we try another larger prime
9 ÷ 3 = 3
So 3 is also a member of 72’s prime factorization! However, we’re not done. We need to divide the last quotient…
3 ÷ 3 = 1
Don’t miss this step! It's easy to forget to divide that last quotient, but if you remember you'll see the prime factorization of 72 is...
Using a prime factorization calculator like the one here may employ a different algorithm, but the resulting factorization will be the same. It is also possible to arrive at the same prime factorization of 72 by starting from 4 x 18 and then repeating the process for each of those values.
Prime Factorization to a Factor Tree
While prime factorizations are unique, there might be several ways to represent the factor tree for any given prime factorization. In the example above, we discussed how a prime factorization could be determined by dividing small primes, or, in the case of 72’s factorization, by starting with larger composites such as 4 x 18. Either approach produces the same factorization, but the route taken is different.
A factor tree documents the path taken to reach the prime factorization, showing each division step along the way. Each branch in the factor tree shows the split of two factors, which may or may not be primes. If a number is composite, the tree extends below it. Depending on how many possible non-prime factors there are, there may be a large number of different factor trees that could be drawn for the same prime factorization. Dad’s prime factorization calculator produces a factor tree for the prime factorization of 72 as shown below:
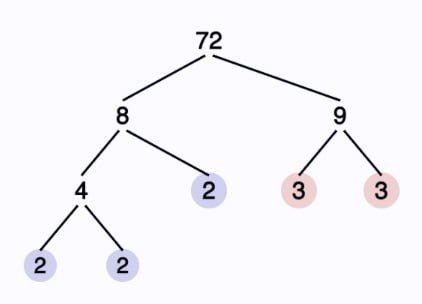
This factorization calculator takes the approach of trying to find factors near the square root. This makes the factor tree shown in the calculator’s answer much clearer, even though this approach may not mimic exactly what you get when producing a prime factorization by hand. Regardless of whether you use the calculator or determine the answer by hand, the factorization will be identical. And the calculator itself is much more interesting to work with, especially with larger integers!
What Can You Do with a Prime Factorization?
Among other things, you can use two prime factorizations produced by this calculator to help determine the least common multiple (LCM) or the greatest common factor (GCF).
This calculator provides some great ways to conceptualize prime factorizations, but if you’re looking for another perhaps less useful but more artistic perspective, be sure to check this link out…
http://www.datapointed.net/visualizations/math/factorization/animated-diagrams/More Calculator Resources
There are a number of other calculators on this site designed to help further your explorations of mathematics and number theory... Be sure to check a few of them out!
Apart from the prime factorization calculator on this page, you can find other math calculators in the ‘Tools’ menu in the upper right. Try a few at the links below!