Core Math Worksheets
Fraction Worksheets
Algebra
Other Worksheets
Place Value
Percentages
Rounding Numbers
Ordering Numbers
Standard, Expanded, Word Form
Mean Median Mode Range
Ratio Worksheets
Probability Worksheets
Roman Numerals
Factorization, GCD, LCM
Prime and Composite Numbers
Pre-Algebra
Geometry Worksheets
Blank Clocks
Telling Analog Time
Analog Elapsed Time
Greater Than and Less Than
Money
Arithmetic Sequences
Geometric Sequences
Venn Diagram
Graph Worksheets
Measurement & Conversions
Patterns and Puzzles
Color by Number
Holiday & Seasonal
Early Learning
Printables
Calculators
Math Worksheets by Grade
Worksheet News
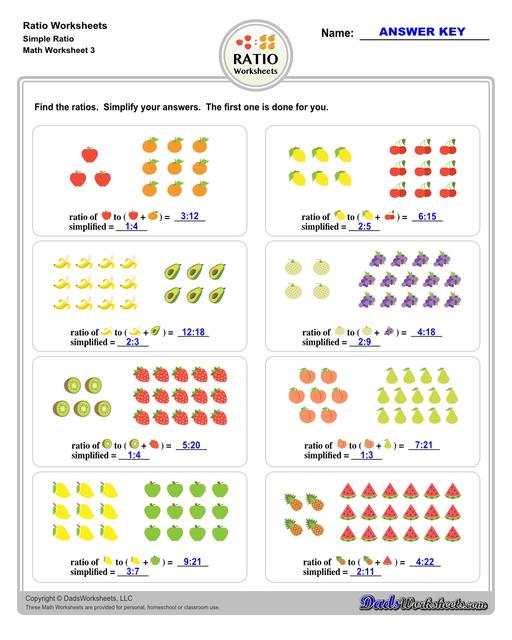
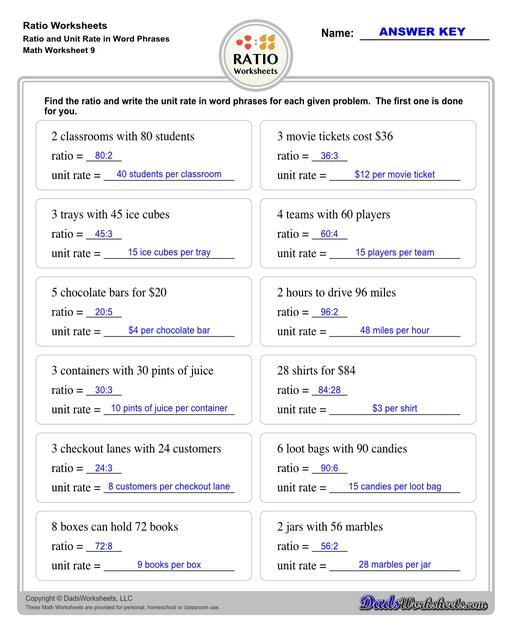
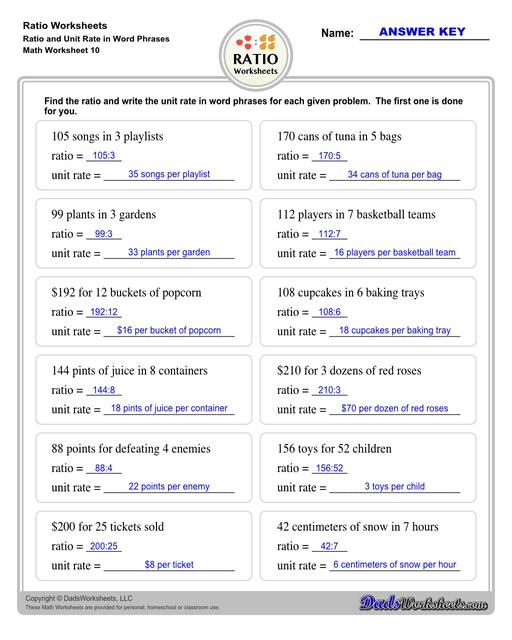
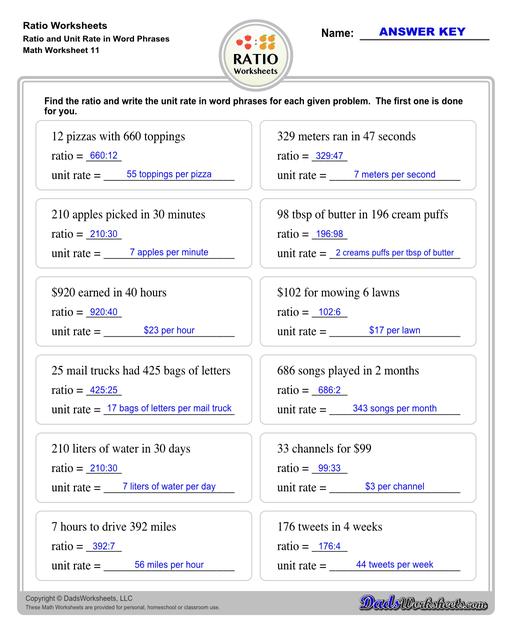
Ratio Worksheets
Ratio worksheets including relating visual quantities, ratio word problems, rate and ratio problems and finding equivalent ratios. These PDF worksheets are designed for 3rd through 6th grade students and include full answer keys.
Visual Ratio Worksheets
Equivalent Ratios Worksheets
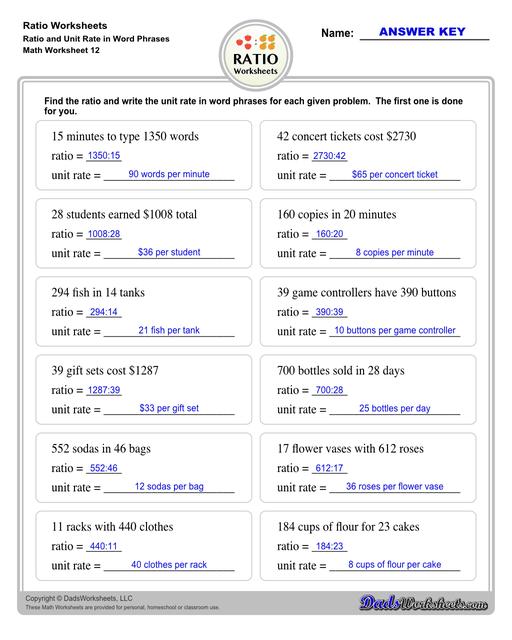
Describing Rates and Ratios
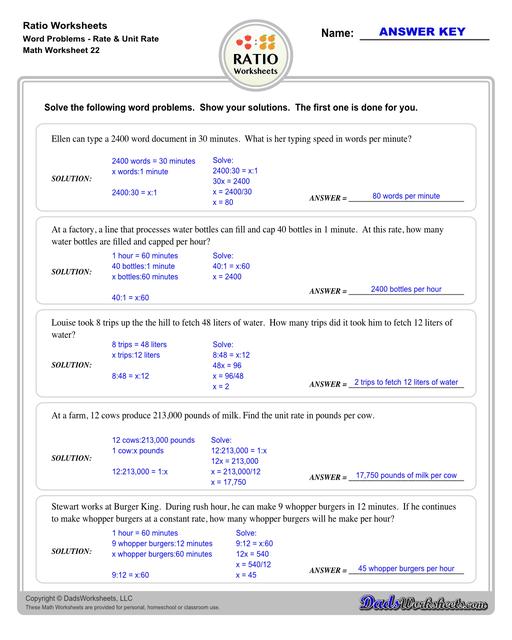
Ratio Word Problem Worksheets
What Is A Ratio?
A ratio is the relationship or comparison between two numbers of the same unit. It is used to indicate how big or small a quantity is when compared to another. For ratios to have meaning you must know what is being compared and the units that are being used.
For example, there are 2 apples and 4 oranges in a fruit basket. We are comparing 2 pieces of apples to 4 pieces of oranges that is in the fruit basket. A general ratio may say “parts” for the units. In our example, the unit that we will use is “pieces” or simply just apples and oranges (2 pcs of apples, 4 pcs of oranges; or 2 apples, 4 oranges).
We write this ratio in three different ways:
- Using the : symbol
- As a fraction
- Using the word “to”
Please refer to the chart below…

No matter how a ratio is written, it is important that it be simplified down to the smallest whole numbers possible, just as with any fraction. When simplifying ratios, we use the highest common factor or HCF (otherwise known as the greatest common factor or GCF) of each of the numbers in the ratio. The term “simplest form” is the same as “lowest form” in ratio and fraction.
For the example above, the highest common factor or greatest common factor would be 2 as we can divide both 2 and 4 by 2.
Solving Ratio Problems
Ratios can be classified into two types. One is part to part ratio and the other is part to whole ratio. A part-to-part ratio shows how one part relates to another part, and a part-to-whole ratio shows how one part relates to the whole. Ratios like these are much more common than you might think.
Let’s use the same example above: There are 2 apples and 4 oranges in a fruit basket.

Part-to-part ratio is shown as follows:
- The ratio of apples to oranges is 2:4.
- The ratio of oranges to apples is 4:2.
Whereas, the part-to-whole ratio that denotes the relationship between apples or oranges to all the fruits in the basket is as follows:
- The ratio of apples to all fruits is 2:6
- The ratio of oranges to all fruits is 4:6
Since there are 2 apples and the total number of fruits in the basket is 6 (2 apples + 4 oranges), the ratio of apples to the all the fruits is 2:6. We use the same method with oranges. There are 4 oranges and the total number of fruits in the basket is 6 (2 apples + 4 oranges), the ratio of oranges to the all the fruits is 4:6.
Now that we know how to solve and write simple ratios, let’s discuss equivalent ratios.
Equivalent Ratios
Equivalent ratios are equal in value to each other. They are similar to equivalent fractions. If the “antecedent” or the first term, and the “consequent” or the second term of a given ratio are multiplied or divided by the same number other than zero, it gives an equivalent ratio.
For example, when the antecedent and the consequent of the ratio 2:4 are multiplied by 2, we get, (2 × 2) : (4 × 2) or 4:8. Here, 2:4 and 4:8 are equivalent ratios.

Similarly, when both the terms of the ratio 2:4 are divided by 2, it gives 1:2, and 4:8 divided by 2, it gives 2:4. Here, 1:2 and 2:4 are equivalent ratios as well.
Take note that in equivalent ratios, if you multiply or divide both the numbers of the ratio by the same number, you get an equivalent ratio.
Another tip when working with equivalent ratio is to use its fraction form. This way, you can easily find equivalent ratios in higher terms, ratios in lower terms, and a missing term.
To find equivalent ratios in higher terms, multiply each term of the ratio by the same number. To find equivalent ratios in lower terms, divide each term of the ratio by the same number.
To find a missing term or an unknown value, follow these simple steps:
- Step 1: Do the cross multiplication of known values
- Step 2: Divide the product by the unknown value.
- Step 3: Check your answer by doing the cross multiplication. If the results are equal, then your answer is correct.
Ratio Word Problems
Ratios are what we use to compare certain number values. People everywhere use ratios and they are often used in many real-world situations, which makes it a valuable skill to master. It helps us to simplify many of our interactions by putting numbers into perspective. Ratios are used in discounts, budgeting, and coupons at grocery stores. Understanding ratios would also enable student to understand interest on loans and how they are paid off. Let’s take a look at a few word problems, and practice working through them.
Example 1: In a class, there are 12 boys and 16 girls. What is the ratio of boys to girls?
Alright, so let’s look at our problem, and see what it is asking us to find, and write out the information that we have been given.
So, there are 12 boys and 16 girls. Let’s write that down.
Now, the question is asking us to find the ratio of boys to girls. Well, we have 12 boys, and 16 girls, which gives us a ratio of 12:16. Note that when writing ratios, we write down what is mentioned first. In our example, “boys” is mentioned before “girls”.
The ratio of boys to girls is 12:16. Let’s look at another word problem.
Example 2: The ratio of girls to boys in a swimming club is 2:3. There are 18 girls. How many boys are there in the club?
Let’s start off the same way that we did our last problem. Read through the problem, write down what is given, and find out what is being asked.
We have all of our information given in the problem, but what are we looking for? It says that the ratio of girls to boys is 2:3 and that there are 18 girls. So, we need to find how many boys there are. How do we do that? We write the formula as follows:

To find a missing term or an unknown value, follow these steps I mentioned earlier:
Step 1: Do the cross multiplication of known values

Step 2: Divide the product by the unknown value.

Step 3: Check your answer by doing the cross multiplication.

The answer is correct because the results are equal. 2x27 equals to 54, and 3x18 also equals to 54.
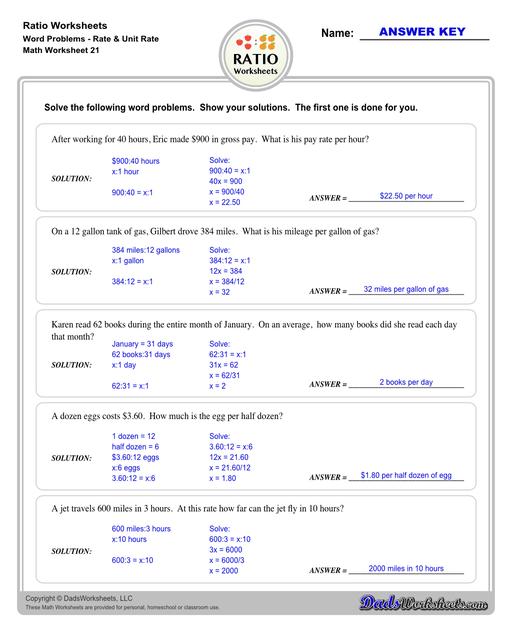
Let’s try a word problem that involves rate and unit rate this time…
Rate is a ratio between two things that have different units of measure, while a Unit Rate describes the ratio of two different units for the quantity of one. We say that when the denominator in rate is 1, it is called Unit Rate.
Example 3: After working for 40 hours, Eric made $900 in gross pay. What is his pay rate per hour?
Again, read through the problem, write down what is given, and find out what is being asked.
To solve, we'll ignore the units ($ and hour) and focus just on the number part for a bit. Divide 900 by 40. You get 22.50. Eric’s pay rate is $22.50 per hour.