Core Math Worksheets
Fraction Worksheets
Algebra
Other Worksheets
Place Value
Percentages
Rounding Numbers
Ordering Numbers
Standard, Expanded, Word Form
Mean Median Mode Range
Ratio Worksheets
Probability Worksheets
Roman Numerals
Factorization, GCD, LCM
Prime and Composite Numbers
Pre-Algebra
Geometry Worksheets
Blank Clocks
Telling Analog Time
Analog Elapsed Time
Greater Than and Less Than
Money
Arithmetic Sequences
Geometric Sequences
Venn Diagram
Graph Worksheets
Measurement & Conversions
Patterns and Puzzles
Color by Number
Holiday & Seasonal
Early Learning
Printables
Calculators
Math Worksheets by Grade
Worksheet News
Properties of Multiplication
If you are looking for multiplication practice focused on the distributive property, associative property or the commutative property then these properties of multiplication worksheets have you covered. Learn how to use multiplication properties to simplify equations or in reverse for factoring.
Associative Property of Multiplication
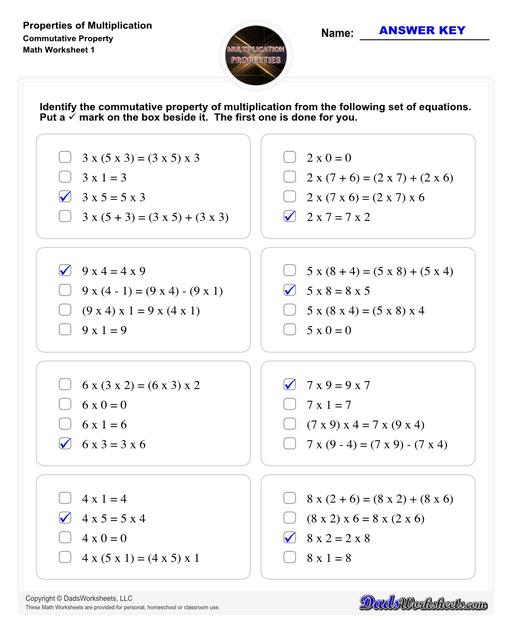
Commutative Property of Multiplication
Distributive Property of Multiplication
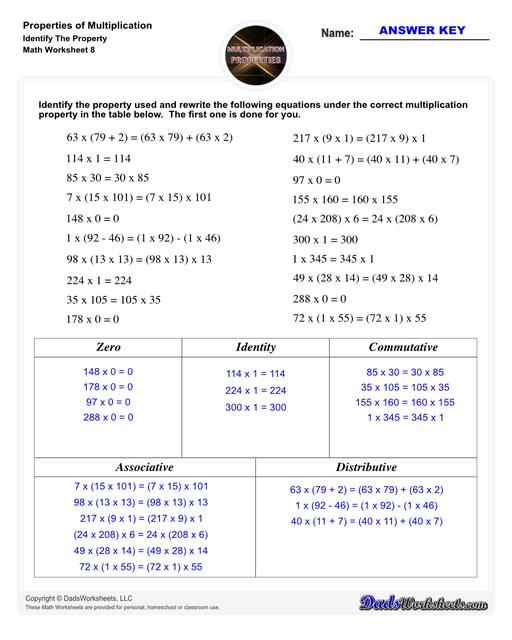
Identify the Property of Multiplication
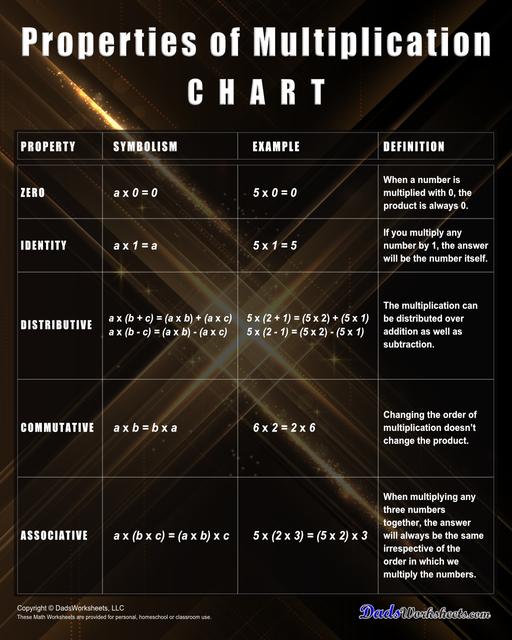
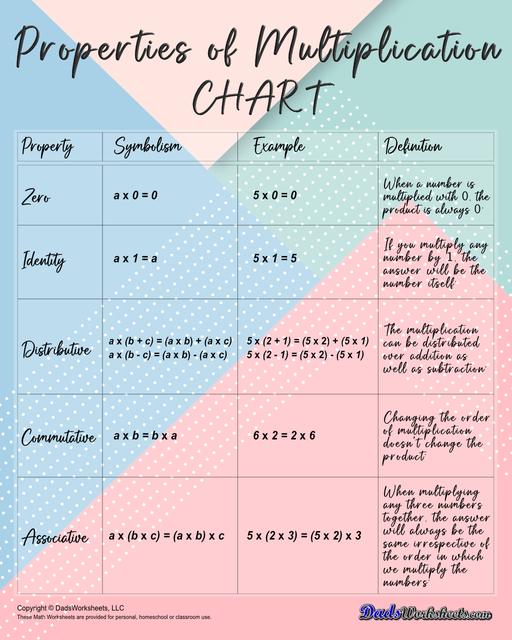
The properties of multiplication anchor chart on this page explains the distributive property, associative property or the commutative property of multiplication. When learning how to simplify or factor equations, these having one of these anchor charts on hand will help students master these very common algebraic steps.
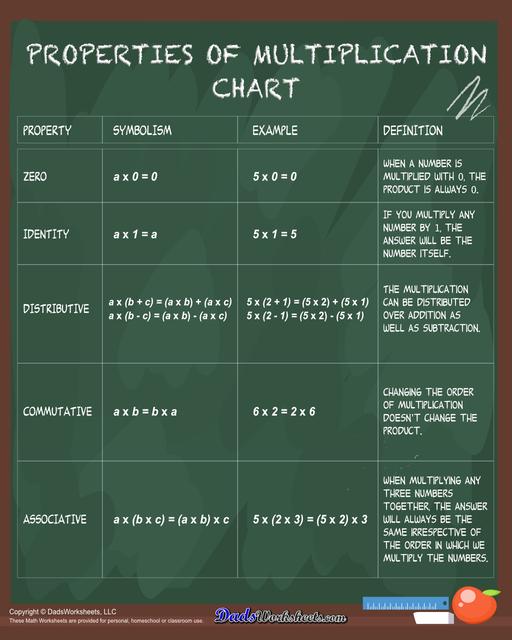
Properties of Multiplication Anchor Chart
Properties of Multiplication
The worksheets on this page will help students identify and master the differences of the five properties of multiplication. The first set of worksheets start with identifying the properties based on given equations. Other sets of worksheets will have 4 versions for each multiplication property. This is a mix of multiplication problems where the order of factors changes and a variety of numbers are given so students will recognize the pattern that the product remains the same regardless of the order of multiplication. All with answer keys!
What Are the Properties of Multiplication?
Multiplication is a fundamental operation in mathematics that involves combining groups of numbers to find their total quantity efficiently. Understanding the properties of multiplication serves a crucial role for developing a solid foundation in mathematics and for solving more complex mathematical problems. In this article, I will help you explore the five fundamental properties of multiplication one by one: the identity property, zero property, commutative property, associative property, and distributive property. For quick reference, you may also print this Properties of Multiplication Chart that I have created for you.
Identity Property
The identity property of multiplication, also known as the multiplicative identity property states that any number multiplied by 1 equals itself. In other words, the product of any number and 1 is always equal to the original number. For example, 8 × 1 is equal to 8.
Mathematically, the identity property of multiplication can be stated as follows:
Here's an example to illustrate the identity property of multiplication:
Consider the expression: 8 × 1
According to the identity property of multiplication, the product is always the original number:
Similarly, the identity property holds true for any other number multiplied by one. For example:
In each case, the product is always the original number, regardless of the value of the other number being multiplied.
Zero Property
The zero property of multiplication states that any number multiplied by 0 equals 0. In other words, the product of any number and 0 is always 0. For example, 9 × 0 is equal to 0.
The zero property of multiplication can be stated as follows:
Here's an example to demostrate the zero property of multiplication:
Consider the expression: 15 × 0. ccording to the zero property of multiplication, the product is always zero:
Similarly, the zero property holds true for any other number multiplied by zero. For example:
In each case, the product is always zero, regardless of the value of the other number being multiplied.
Commutative Property
The commutative property of multiplication is the simplest of multiplication properties. It states that changing the order of the factors does not change the product. In other words, when multiplying two numbers, the result is the same regardless of the order in which the numbers are multiplied. For example, 3 × 4 is equal to 4 × 3. The product is 12 regardless of the order the equation is written.
The commutative property of multiplication can be stated as:
Here's an example to illustrate the commutative property:
Consider the multiplication equation: 7 × 5 = 5 × 7. According to the commutative property, we can reverse the order of the factors and still obtain the same product:
Let's compute if the statement is true:
As illustrated, the product is the same (35) regardless of the order of multiplication, which corroborates the commutative property of multiplication.
Tip: We apply the commutative property when we learn the multiplication tables. Knowing that the order of the factors does not change the product, you do not need to learn entire tables.
Associative Property
The associative property of multiplication states that the grouping of factors does not affect the product. This means that when multiplying three or more numbers, the result is the same regardless of how the numbers are grouped. For example, (2 × 3) × 4 is equal to 2 × (3 × 4). Again, The product is 24 regardless of the order the equation is written.
The associative property of multiplication can be stated as
Here's another example to illustrate the associative property
Consider the multiplication expression: 6 x 5 x 4. Using the associative property, we can group the factors in two different ways:
Now, let’s check if the statement is true:
As we can see, regardless of how we group the factors, the product remains the same, which confirms the associative property of multiplication.
Moving on to the last property, the distributive property of multiplication. Continue reading below…
Distributive Property
The distributive property of multiplication explains how multiplication distributes over addition. It states that multiplying a number by the sum of two or more numbers is the same as multiplying the number by each addend individually and then adding the products. It is generally used for fast and easier multiplications. For example, 3 × (4 + 2) is equal to (3 × 4) + (3 × 2).
The distributive property can be stated as follows:
This property means that when you multiply a number by the sum or difference of two other numbers, it's the same as multiplying the number by each of the other numbers and then adding or subtracting the products.
Let’s further discuss the example mentioned earlier to illustrate the distributive property:
Consider the expression: 3 × (4 + 2). According to the distributive property, we can distribute the multiplication over addition:
Let's compute and check if the statement is true:
As shown, both expressions yield the same result (18), which confirms the distributive property of multiplication over addition.
Similarly, the distributive property also holds for multiplication over subtraction. Let’s change the (+) positive sign inside the pharenthesis into a (-) negative sign to check.
Consider the expression: 3 × (4 - 2). According to the distributive property, we can distribute the multiplication over subtraction:
Let's compute and check if the statement is true:
Again, both expressions yield the same result (6), confirming the distributive property of multiplication over subtraction.
Difference Between Identity Property and Zero Property of Multiplication
The Identity property of multiplication should not be mistaken for the Zero property of multiplication. Here are a few things to note:
- The Identity Property involves multiplying a number by 1, whereas the Zero Property involves multiplying a number by 0.
- The Identity Property emphasizes the preservation of value, while the Zero Property highlights the annihilation of value, reducing it to 0.
- When we multiply any number by zero, the answer is always 0, whereas when we multiply any number by one, the answer is always the number itself.