Core Math Worksheets
Fraction Worksheets
Algebra
Other Worksheets
Place Value
Percentages
Rounding Numbers
Ordering Numbers
Standard, Expanded, Word Form
Mean Median Mode Range
Ratio Worksheets
Probability Worksheets
Roman Numerals
Factorization, GCD, LCM
Prime and Composite Numbers
Pre-Algebra
Geometry Worksheets
Blank Clocks
Telling Analog Time
Analog Elapsed Time
Greater Than and Less Than
Money
Arithmetic Sequences
Geometric Sequences
Venn Diagram
Graph Worksheets
Measurement & Conversions
Patterns and Puzzles
Color by Number
Holiday & Seasonal
Early Learning
Printables
Calculators
Math Worksheets by Grade
Worksheet News
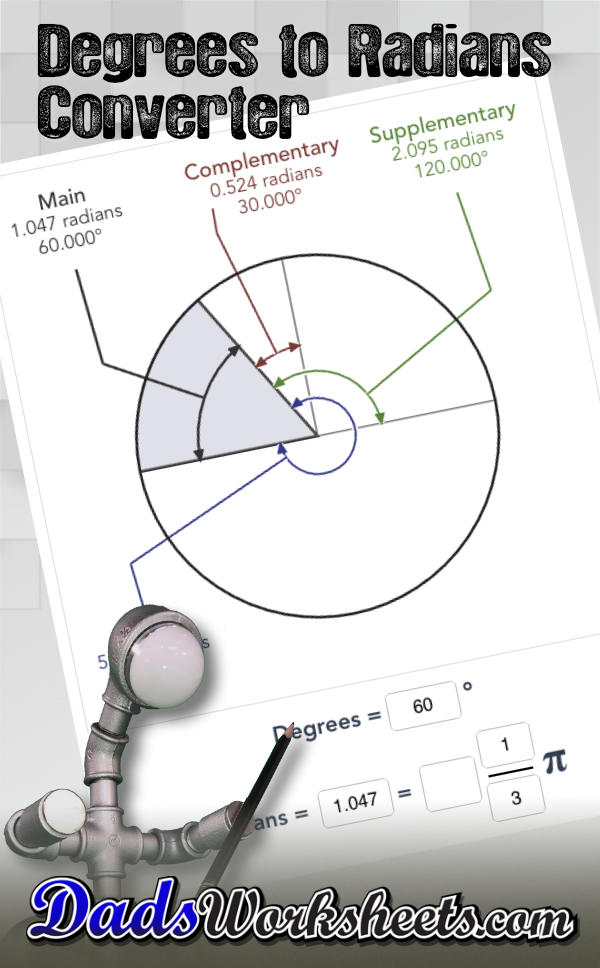
Degrees to Radians Converter
How to use the Degrees to Radians Converter
This calculator converts degrees to radians, or radians to degrees. The calculator also calculates complementary and supplementary angles and shows a combined representation of the related angles so that they can be immediately visualized. The calculator automatically converts from degrees to radians when you enter a new value.
What are Degrees?
When we measure the angle between two lines, that measurement is providing the amount of rotation necessary to make the slope of one line match that of the other. The word degree in its most general usage means "amount" but when measuring an angle, the word degree is a unit of rotation.
Degrees in a Circle
A full rotation (or a turn) would correspond to a complete circle, or exactly 360 degrees of rotation. If you wonder about the seemingly odd choice of using 360 degrees to represent a full rotation, you can probably blame the Babylonians. Some ancient number systems were based on units like 12 and 60. Examples of how this carried forward into modern life is the 12 months of the calendar and 24 hours in the day (12 hours of day, 12 hours of night). Another example is the choice of 360 as the units of measurement complete circle. 360 factors neatly by both 12 and 60, and you can inscribe six equilateral triangles (which have exactly 60 degrees at each angle) in a circle.
What are Radians?
While degrees are familiar to most people, for many applications it is more convenient to work in a different unit of angular measurement called radians. To understand the value of a radian, it's useful to remember the formula for the circumference of a circle...
Circumference of a Circle
The circumference relates directly to a full rotation, and travelling around the circumference is conceptually similar to rotating a point through 360 degrees around the circle's origin. If we imagine a circle with a radius of one unit (a unit circle) then this path is equivalent to exactly 2π units. And in fact, those arbitrary circumference units are radians, and there are exactly 2π radians in a full rotation.
Expressing rotation in terms of radians simplifies a number of other trigonometric calculations, but because radians are expressed in terms of pi they may feel less useful in practical applications (for example, setting the angle on a saw blade when you're cutting a piece of wood.) That's where this degrees to radians converter comes into play!
Radians in a Circle
This degrees to radians converter allows you to enter radians either as a decimal value or as a fraction of pi, and it will calculate the alternate radians representation as well as the value in degrees appropriately.
How to Convert Degrees to Radians
There are two simple approaches to converting degrees to radians, one deals with decimal radians and the other with radians expressed as a fraction of pi.
Because the number of degrees in a circle is a transcendental number and has an infinite decimal expansion, there is not an exact conversion from degrees to decimal radians. However, a reasonable approximation is to use a decimal constant of sufficient precision for whatever calculation you are trying to perform...
Degrees to Radians as a Decimal
However, by expressing radians as a fraction of pi, you can calculate a precise fraction multiplied by pi. Recall that a full circle (360° of rotation) is exactly 2π radians, so 180° is π radians. Therefore, one degree is 1/180th of π radians...
Degrees to Radians as a Fraction of Pi
Example: Convert 36 Degrees to Radians
Any of these methods for converting degrees to radians are similar and based on the idea that degrees are π/180 radians.
How to Convert Radians to Degrees
Converting radians to degrees is similar, and we can use invert the constants used in degrees to radians conversion...Radians to Degrees
Degrees to Radians Updates
| Date | Description |
|---|---|
| 06/3/2019 | Initial version of the Degrees to Radians converter. |
| 01/29/2021 | Updated to new calculator format. |
