Core Math Worksheets
Fraction Worksheets
Algebra
Other Worksheets
Place Value
Percentages
Rounding Numbers
Ordering Numbers
Standard, Expanded, Word Form
Mean Median Mode Range
Ratio Worksheets
Probability Worksheets
Roman Numerals
Factorization, GCD, LCM
Prime and Composite Numbers
Pre-Algebra
Geometry Worksheets
Blank Clocks
Telling Analog Time
Analog Elapsed Time
Greater Than and Less Than
Money
Arithmetic Sequences
Geometric Sequences
Venn Diagram
Graph Worksheets
Measurement & Conversions
Patterns and Puzzles
Color by Number
Holiday & Seasonal
Early Learning
Printables
Calculators
Math Worksheets by Grade
Worksheet News
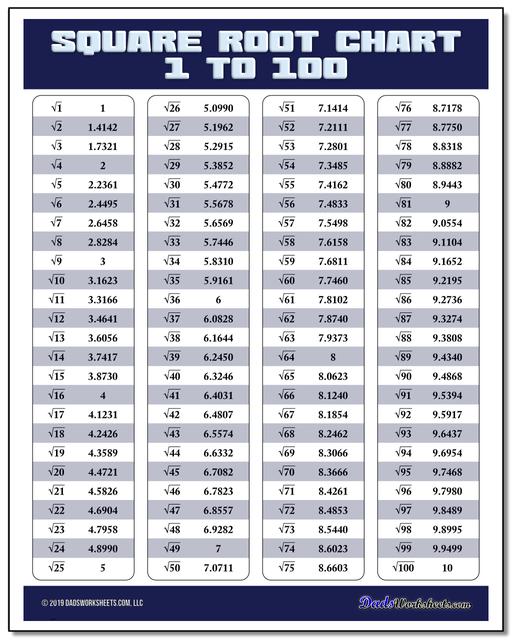
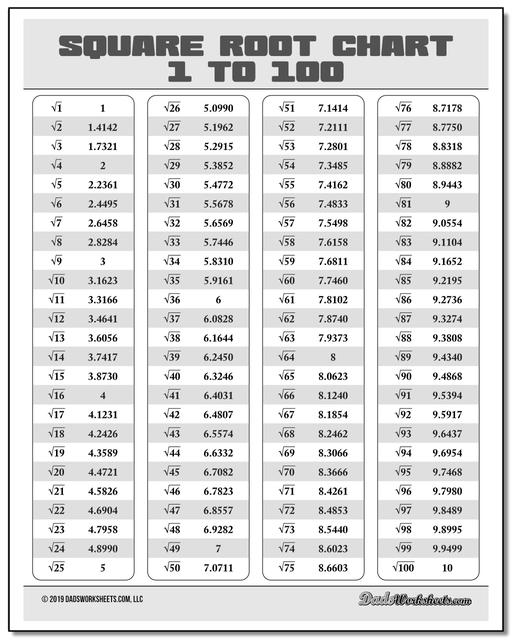
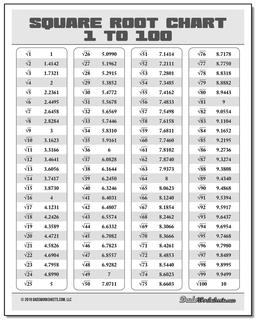
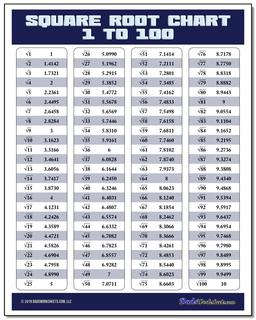
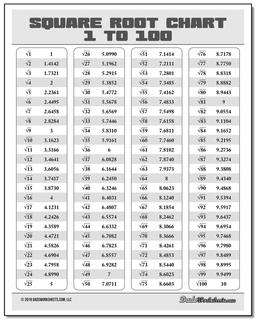
Square Root Chart
Whether you're looking for a list of perfect square roots, or a complete table of square roots from 1 to 100, a square root chart from this page will have your radicals covered! There are both color and black and white versions of the charts in printable PDF form.
Square Root Chart
Printable Square Root and Perfect Square Charts
The finely crafted charts on this page are ready to send straight to your high-resolution printer and would make a fine addition to your student's basic geometry and algebra folders.
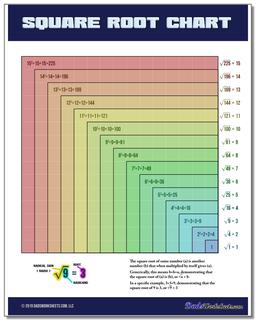
The colorful chart with the perfect squares from 1 to 15 not only have a visual representation of the square area associated with each root calculation, but also show the names of the parts of a square root expression (radical sign, radicand and root) and a brief description of how a specific square multiplication problem relates to a square root equation.
What are Square Roots?
A good way to explain square roots to students is to describe it as the reverse of multiplying a number by itself. Students are often familiar with functions that complement each other (for example addition and subtraction.) Using this framework to describe finding roots as a special reversal of a multiplication problem is a great mental shortcut for explaining not just square roots, but different radix roots as well.
The square root of some number (a) is another number (b) that when multiplied by itself gives (a). Generically, this means bxb=a, demonstrating that (b) is the square root of (a) or in a specific example, 3x3=9, demonstrating that 3 is the square root of 9.
While we usually learn about square roots in the context of integers, we can also find the square roots of numbers that are not integers. For example, the square root of 10 is a decimal number close to 3.16227 (you can check this by multiplying that number times itself on a calculator and you'll get a value very close to 10.)
So What makes a Perfect Square Root?
When you multiply a positive integer by itself, it is a perfect square. The product of that multiplication will be an integer, and square root of that value will be the original number which was also an integer. These whole integer roots are known as perfect square roots.
So as you probably guessed, an imperfect square is going to have a square root that is not an integer (it has a decimal or fractional part) like the square root of 10 we calculated above. In fact, these roots will all be irrational numbers with decimal values that continue forever. Because of this, imperfect square roots are rounded to some degree of decimal precision for practical applications. This is a really interesting math topic that you can dive into here if you're interested in learning more.
How Are Square Roots Calculated?
Because square roots for most numbers are irrational, the method for calculating them precisely is a bit cumbersome. The procedure for calculating square roots of arbitrary numbers is to begin with an estimate and then progressively refine it until you arrive at a value of sufficient accuracy for your needs. You can find more details on how square roots are calculated at Wikipedia and these techniques are essentially what your pocket calculator is doing when you hit the square root key.
The roots in the 1-100 square root chart on this page are rounded to four decimals of precision for the roots of imperfect squares.
What are Higher Order Roots?
Square roots are just the beginning!
A cube root is like a square root, but the root value is multiplied by itself three times to get the 'cube' value. So for example, 2x2x2=8 implies that the cube root of 8 is 2.
You can find higher order roots beyond just squares and cubes, but only those two have special names. For example, the 4th root 16 is 2 since 2x2x2x2 (a total of 4 twos multiplied) equals 16. You'll notice this is also 2 raised to the 4th power (an exponent), and you'll see a very clear inverse relationship between nth degree roots and application of exponents to a number.
What is a Principal Root of a Number?
If your kids have been exposed to negative numbers, they know already that two negative numbers multiplied together yield a positive result. Because of this, there are actually two square roots of a positive number... One is positive and one is negative. For example, -2x-2=4 so the square root of 4 could be 2 or -2. We distinguish the positive root from the negative root by calling it the principal root of the number.
So What About Roots of Negative Numbers?
If a square root can be a real number (either an integer if it is the root of a perfect square or a decimal if it is the root of an imperfect square), we know we will get a positive result by multiplying that number by itself. It's not possible to get a negative square result by multiplying the same number times itself because you're multiplying either a positive times a positive, or a negative times a negative... Both always give you a positive product.
The way we get to square roots of negative numbers is to introduce an entirely new type of numbers, and of course since we call the sets of integers and decimal numbers real numbers we can clevery invent a new set of imaginary numbers to do something else entirely.
Imaginary numbers introduce the unit imaginary number i that is explictly the square root of -1. By introducing this imaginary unit, the squary root of a negative number can be computed as a value with an imaginary result. For example, the square root of -4 becomes 2i.
What is Pythagora's Constant?
Pythagora's Constant is the square root of 2. Because 2 is not a perfect square, it's square root is an irrational number. This number shows up in many geometric operations, but it really is just a square root.
On the square root chart above, you can see the value for the square root of 2 is approximately 1.4142, and this is a good constant to memorize.
Worksheet History