Core Math Worksheets
Fraction Worksheets
Algebra
Other Worksheets
Place Value
Percentages
Rounding Numbers
Ordering Numbers
Standard, Expanded, Word Form
Mean Median Mode Range
Ratio Worksheets
Probability Worksheets
Roman Numerals
Factorization, GCD, LCM
Prime and Composite Numbers
Pre-Algebra
Geometry Worksheets
Blank Clocks
Telling Analog Time
Analog Elapsed Time
Greater Than and Less Than
Money
Arithmetic Sequences
Geometric Sequences
Venn Diagram
Graph Worksheets
Measurement & Conversions
Patterns and Puzzles
Color by Number
Holiday & Seasonal
Early Learning
Printables
Calculators
Math Worksheets by Grade
Worksheet News
Probability Worksheets
Probability worksheets including simple coin tosses, spinners and dice throws. These worksheets also include vocabulary for solving probability problems as percentages, decimals or fraction values representing that measurement of possible outcomes for simple problems.
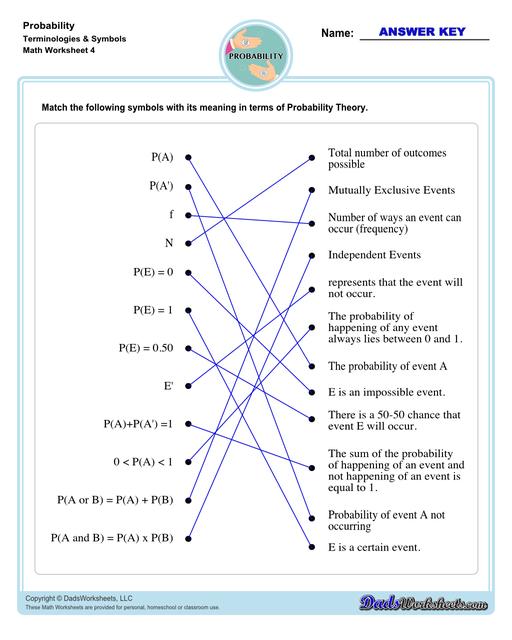
Probability Vocabulary
Probability for Drawing Cards
Picking Numbers Probability Worksheets
Rolling Dice Probability Worksheets
Probability Spinner Worksheets
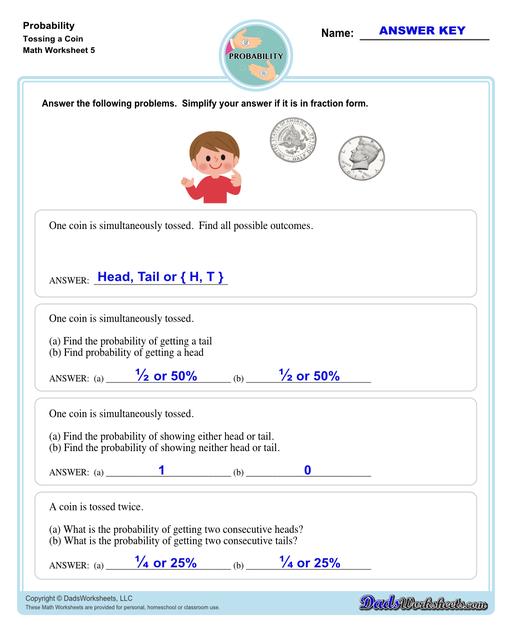
Coin Toss Probability Worksheets
What Is Probability Theory?
Probability is the branch of mathematics that deals with random events and measuring how likely they are to occur. In Probability Theory, the probability of happening of any event always lies between 0 and 1, where 0 represents that the event will not happen and 1 means that an event is certain.

A perfect example of a probabilistic experiment is a fair coin toss, in which the two possible outcomes are heads or tails. In this example, the probability of flipping a head or a tail is one-half. In an actual series of coin tosses, we may get more or less than exactly one-half or 50% heads. But as the number of flips increases, the long-run frequency of heads is bound to get closer and closer to 50%. A Probability Chart like this can be a helpful reference if you’re just starting to learn about probability.
Note: A coin is said to be a “fair coin” when it behaves like a generic coin. Fair coin has the same outputs as the generic coin. For example, a fair coin has two outcomes: one Head and one Tail. In short, a fair coin is by definition a coin with an equal probability of heads and tails. Another term used in Probability for a “fair coin” is “unbiased coin”.
Suppose the chances of getting a head in tossing a fair coin once is one-half, we can write this probability in three different ways:
- As a fraction
- As a percentage
- As a ratio
Please refer to the sample illustration below…

Solving Probability Problems
The general formula to determine the probability is:

Where,
Let’s try an example.
Example 1: A fair coin is tossed once. What is the probability of getting a head?
Solution:

Let P(A) be the probability of getting a Head Number of favorable outcomes or heads in coin toss = 1, the Total number of favorable outcomes = 2 (Heads, Tails)
Now, by using the formula, the probability of getting heads from tossing the coin once is:
So we can say that the probability of getting a head is 1/2 or 50%.
Let’s try another example using a fair die this time…
Example 2: A fair die is rolled once. Find the probability of getting an even number.
Solution:

The sample space has 6 favorable outcomes: S = {1,2,3,4,5,6}
Let A denote the event that we get an even number on tossing the die. It can occur in 3 possible ways... A = {2,4,6} So, the number of favorable outcomes = 3, and the total number of events in a sample space = 6. Hence, the probability of getting an even number from rolling a die once is:
The probability of getting an even number is 1/2 or 50%.
Let’s proceed to our third example. This time we will determine the probability of outcomes involving a deck of cards.
Example 3: A card is drawn at random from a 52-deck card. What is the probability of getting an Ace?
Solution:
The number of Ace cards in a deck of cards = 4, total number of cards in a deck = 52. So, the number of favorable outcomes = 4 and the total number of favorable outcomes = 52. The probability of getting an ace from the deck of cards is:
So we can say that the probability of getting an ace is 1/13 or 7.69%.
Important Terms in Probability
There are some basic terminologies associated with probability theory that aid in the understanding of this field of mathematics. Here are some of the most important ones…
Experiment - in probability theory, this can be defined as a trial that is repeated multiple times in order to get a well-defined set of possible outcomes. Tossing a coin is an example of a random experiment.
Trial - one round of an experiment. For example, each time you would flip a coin is a trial.
Outcome - the result of a trial. For example, if you flip a coin and it lands on heads, heads is the outcome.
Event - a collection of outcomes within an experiment that forms a subset of the sample space. For example, getting a Heads in tossing a coin is an event.
Sample Space - can be defined as the set of all possible outcomes that result from conducting a random experiment. For example, the sample space of tossing a fair coin is Heads and Tails.
Types of Probability
The three major types of probability that are commonly used are the following:
Theoretical - also called Classical Probability, is the type of probability that is based on the possible chances of something happening. For example, if a coin is tossed, the theoretical probability of getting a head will be 1/2 or 50%.
Experimental - also called Empirical Probability, is the type of probability that is based on the observations of an experiment. For example, if a coin is tossed 5 times and Heads is recorded 2 times then, the experimental probability for heads is 2/5 or 40%.
Axiomatic the type of probability that is based on a set of axioms
Other types of Probability:
Conditional - the likelihood of an event or outcome occurring based on the occurrence of a previous event or outcome
Subjective - considers an individual’s own belief of an event occurring. It models the reality that often people do differ in their judgments of probability
Importance of Probability
We use or see probability all around us in our daily lives. Without knowing, we use probability every day to make decisions about things with unknown outcomes. We may unknowingly perform mathematical calculations with theoretical or experimental probability, or we may make decisions with subjective probability in mind. Some real-life examples where people use probability are weather forecasts, strategies for competitions and games, analyzing which insurance policy to get, while playing games, etc. Whether it's the weather or the next roll of the dice, no one knows for sure what the future holds. But we can use different types of probability strategies to come up with our best guess.
Things To Remember in Probability Theory
- Probability theory is a branch of mathematics that deals with the probabilities of random events.
- The concept of probability in probability theory gives the measure of the likelihood of the occurrence of an event.
- The probability of an event can only be between 0 and 1 and can be written as a percentage, fraction, or ratio.
- The probability of 0 represents that the event will not happen or that it is an impossible event.
- The probability of a sure event is always equal to 1.
- In probability theory, all the possible outcomes of a random experiment give the sample space.
- Probability theory uses important concepts such as random variables, and cumulative distribution functions to model a random event and determine various associated probabilities.
- A tree diagram in probability is a visual representation that helps in finding the possible outcomes or the probability of any event occurring or not occurring.
- For each toss of a fair coin, the probability of getting “Heads” is one-half or 50%.
- When rolling a pair of dice, one die does not affect the outcome of the other die.
- Two events are dependent when the outcome of the first event influences the outcome of the second event.
- A Dependent Event is also known as a Conditional Event.
- Two events are independent when the outcome of the first event does not influence the outcome of the second event.
- Two events are mutually exclusive when two events cannot happen at the same time.
- When the events have the same chances of probability of happening, then they are called Equally Likely Events.
- Two events are said to be complementary when one event occurs if and only if the other does not.
- The complement of an event is the event not occurring.
- Mutually exclusive events never have an outcome in common.
- If an event cannot happen, we call it an Impossible Event.