Core Math Worksheets
Fraction Worksheets
Algebra
Other Worksheets
Place Value
Percentages
Rounding Numbers
Ordering Numbers
Standard, Expanded, Word Form
Mean Median Mode Range
Ratio Worksheets
Probability Worksheets
Roman Numerals
Factorization, GCD, LCM
Prime and Composite Numbers
Pre-Algebra
Geometry Worksheets
Blank Clocks
Telling Analog Time
Analog Elapsed Time
Greater Than and Less Than
Money
Arithmetic Sequences
Geometric Sequences
Venn Diagram
Graph Worksheets
Measurement & Conversions
Patterns and Puzzles
Color by Number
Holiday & Seasonal
Early Learning
Printables
Calculators
Math Worksheets by Grade
Worksheet News
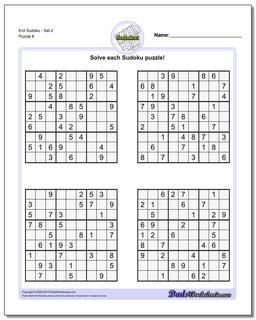
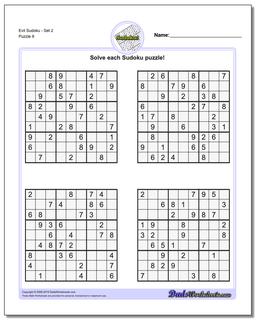
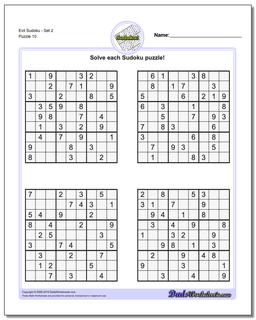
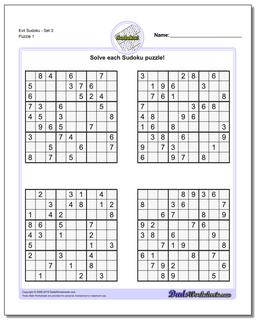
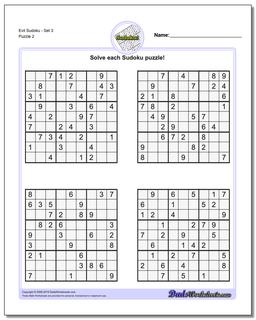
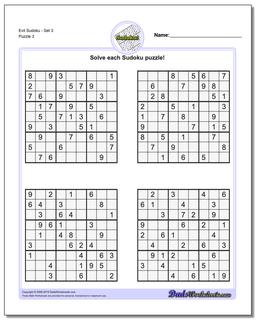
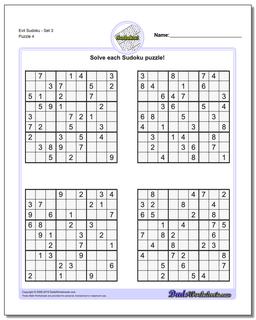
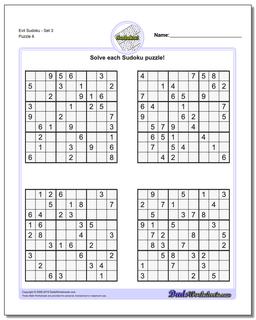
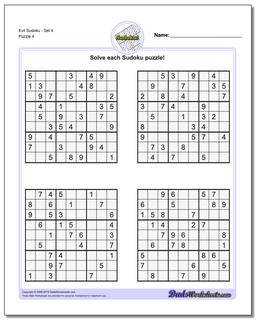
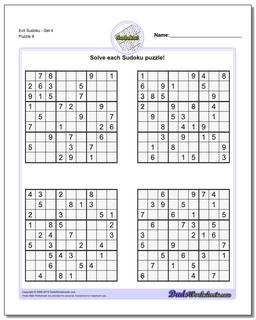
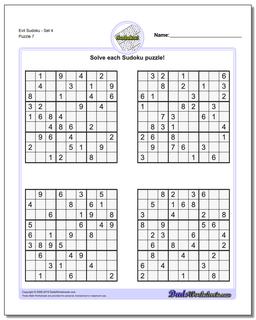
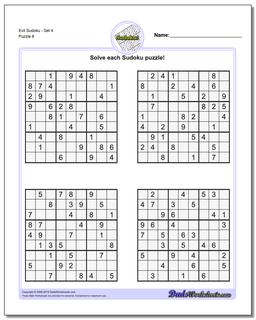
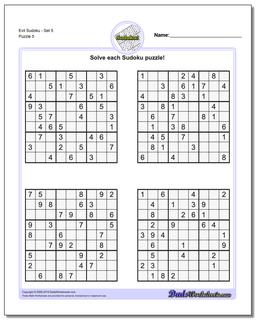
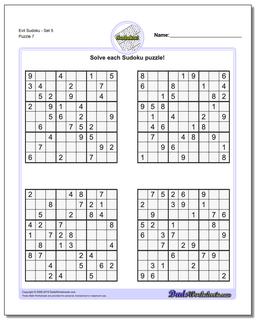
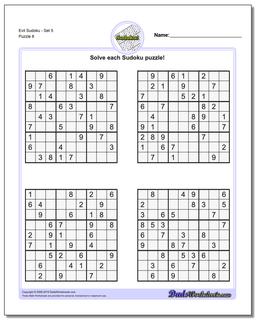
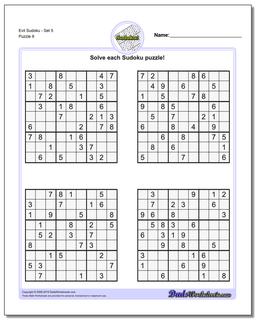
Sudoku - Evil
Recent research has shown that that a valid sudoku puzzle will have at least 17 clues. The evil sudoku puzzles in this section come from Gordon Royle's list of minimal sudoku starting geometries with these challenging starting conditions.
Evil Sudoku - Set 1
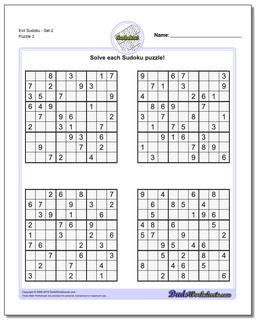
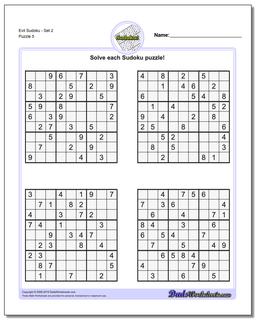
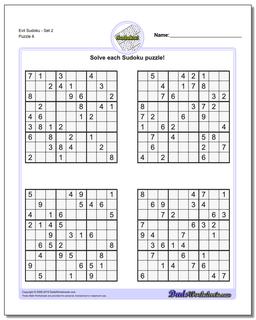
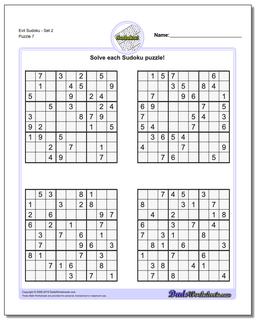
Evil Sudoku - Set 2
Evil Sudoku - Set 3
Evil Sudoku - Set 4
Evil Sudoku - Set 5
Printable Evil Sudoku Puzzles
Evil Sudoku includes some of the most challenging Sudoku puzzles that are mathematically possible. Because a valid sudoku puzzle must have exactly one unique solution, coming up with a sudoku puzzle can often be more challenging than solving one. Each puzzle must meet the constraints required to solve it, but additionally it must be constrained enough to require a unique and specific solution. This is pretty easy if the sudoku has lots of clues because it winds up requiring very specific values in very specific spaces of the solution. But as the number of sudoku clues decreases, these contraints make other solutions much more likely.
Sudoku masters have known for some time that the absolute minimum number of clues a puzzle can have and still be valid is 17. There are still a quite large number of possible puzzles (most variations of equivalent puzzles of the same form) that can be created.
Gordon Royle at the University of Western Australia maintains a repository of N-17 sudoku, and the evil sudoku puzzles in this section are derived from the patterns he provides on his site.
This is a link to his minimum sudoku page, but I also highly recommend the article he wrote here on sudoku complexity for those interested in some of the math, especially a more readable discussion of Gary McGuire's research on the topic.
Regardless of the math behind them, you'll find they call these evil sudoku puzzles because they are hard to solve. Thanks a lot Gordon!